14 Route Assignment

14.1 Introduction

By default, the method SwashSim uses to move vehicles from an entry link to an exit link is based on user-specified turning percentages. That is, when a vehicle exits a link, it gets randomly assigned a turning movement for the next link based on user-specified turning percentages for the link (e.g., 25% left, 55% through, 20% right). For this method, it is not possible to explicitly assign specific percentages of vehicles to travel between a given origin-destination pair. Alternatively, a route assignment method can be implemented. The route assignment method uses an origin-destination (O-D) demand matrix with the user equilibrium (UE) traffic assignment method to specify the full route through the network each simulated vehicle will take.

14.2 Link Performance Function

Route assignment concerns the selection of routes (or paths) between origins and destinations in transportation networks. Since the selection of routes is often based on the link travel time, it is essential to describe the relationship between link travel time and link flow. Link performance functions are often used for this purpose, such as the Bureau of Public Roads (BPR) function shown below (Public Roads (1964)).

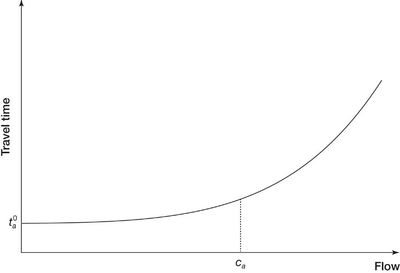
Figure 14.1: BPR Function Example

\[t_\alpha = t_\alpha^0(1 + 0.15(\frac{v_\alpha}{c_\alpha})^{4})\]

\(t_\alpha\) is the average travel time of link \(\alpha\) \(t_\alpha^0\) is the free-flow travel time of link \(\alpha\) \(v_\alpha\) is the traffic volume of link \(\alpha\) \(c_\alpha\) is the capacity of link \(\alpha\)

14.3 User Equilibrium Route Assignment

UE assignment is the most commonly used route assignment. Wardrop (1952) proposed the concept of UE under the assumption that users in a traffic network tend to minimize their travel times, and UE is achieved when no user can reduce his/her travel time by changing routes.

Based on the use of non-decreasing, continuous and differentiable link performance functions, Beckmann, Mcguire, and Winsten (1957) proposed the mathematical programming formulation for UE traffic assignment, which formulated the problem as a convex problem with a convex objective function under linear constraints. Dafermos and Sparrow (1969) applied the Frank-Wolfe algorithm (Frank and Wolfe (1956)) to solve this convex problem.

The Frank-Wolfe algorithm applies an iterative process that involves performing all-or-nothing assignment, updating link volumes, finding optimal direction, updating link volumes, and checking link volume convergence. The terminating condition of the iterative loop process is the convergence of link volumes. Note that the all-or-nothing assignment is basically to find the shortest path (path with the shortest travel time) between each OD pair, and assign all the demand of the OD pair to that shortest path. Below shows the Frank-Wolfe process’ steps and formulas.

Step 0. Initialization. Perform all-or-nothing assignment based on \(t_a = t_a(0), \forall a\). This yields \(x^1\). Set counter \(n:=1\)
Step 1. Update. Set \(t_a^n=t_a(x_a^n),∀a.\)
Step 2. Direct finding. Perform all-or-nothing assignment based on \(t_a^n,\forall a\). This yields (direction) flows yⁿ
Step 3. Line Search. Find \(\alpha_n\) that solves \[min_{0\le\alpha_n\le1} \sum_\alpha \int_0^{x_a^n+\alpha_n(y_a^n - x_a^n)} t_a (\omega)d\omega\]
Step 4. Move. Set \(x^{n+1}=x^n+\alpha_n(y^n-x^n)\)
Step 5. Convergence test. If \(\frac{\sqrt{\sum_\alpha(x_a^{n+1} - x_a^n)^2}}{\sum_\alpha x_a^n} < \epsilon\), stop; otherwise \(n:=n+1\), and go to Step 1.

14.4 XXE

Figure 14.2: BPR Function Example

XXE is a traffic assignment program based on the standard user equilibrium principle, which is defined as: “The travel time between a specified origin and destination on all used routes is the same and is less than or equal to the travel time that would be experienced by a traveler on any unused route.” With a defined network and a given origin-destination matrix, XXE assigns traffic flows by setting up the user equilibrium problem as a mathematical program as shown in Equation 8.8 in Mannering and Washburn (2019). (https://github.com/swash17/XXE)
XXE is a program developed by Scott Washburn and Fred Mannering in 2007. The XXE program implements the Frank-Wolfe approach to solve the UE traffic assignment. The route assignment method calls the XXE program to perform the UE traffic assignment. [https://github.com/swash17/XXE]

14.5 User Equilibrium Path Flow

In order to assign routes to simulated vehicles, the path flow under UE condition is needed. However, while the UE link volumes are unique for a specific network and OD demand matrix, path volumes are not unique in most cases. This project obtains one set of feasible path flow solution as the side product of the Frank-Wolfe approach. During the Frank-Wolfe approach, the path volumes are saved and updated the same way as the link volumes. The XXE program is modified to save and update the path flow during the Frank-Wolfe approach, and output one set of feasible path flow under UE condition.

As the feasible path flow needs to satisfy two constraints:

link volume equals to the sum of all the path volumes that use that link;
OD volume equals to the sum of all the path volumes that are associated with that OD. The following tables show the UE results output from the modified XXE program on a network with four OD pairs, the two tables show that the path flow from XXE satisfy the two constraints.

Link Constraints	Link Volumes	Path Volumes	Difference
9, 10	982.808761	982.81	-0.0012
9, 11	1071.47666	1071.48	-0.0033
10, 9	1099.11443	1099.12	-0.0056
10, 12	813.523343	813.52	0.00334
11, 9	690.170992	690.17	0.00099
11, 12	972.191239	972.19	0.00124
12, 10	874.829008	874.83	-0.001
12, 11	1100.88557	1100.88	0.00557

OD Constraints	OD Demand	Path Volumes
12	750	750.000
13	500	500.000
14	640	640.000
21	700	700.000
23	495	495.000
24	250	250.000
31	350	350.000
32	240	240.000
34	325	325.000
41	575	575.000
42	400	400.000
43	430	430.000